Difference between revisions of "Waveform"
Brad Johnson (talk | contribs) |
Brad Johnson (talk | contribs) |
||
| Line 16: | Line 16: | ||
[[File:Sine 2 wave in-phase graph.png|800px|Two 1kHz sine waves “in-phase”]] | [[File:Sine 2 wave in-phase graph.png|800px|Two 1kHz sine waves “in-phase”]] | ||
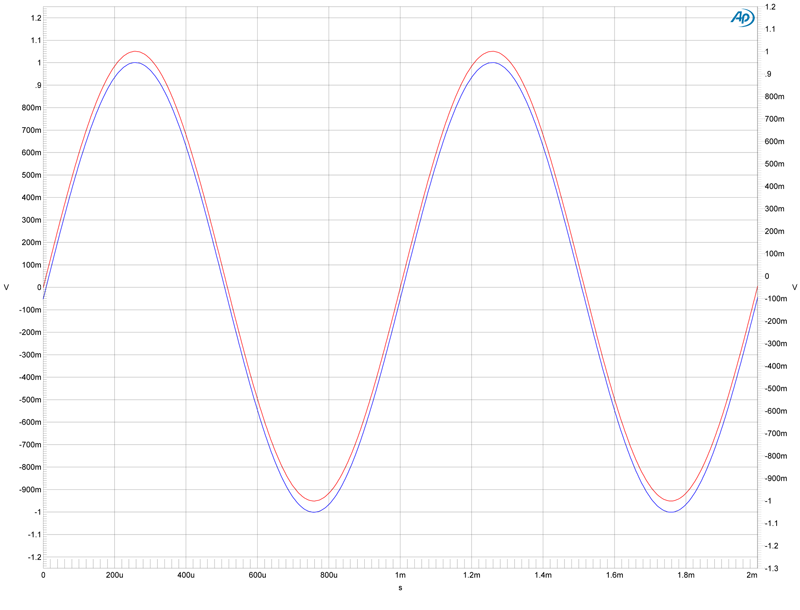
| − | The scale for the blue sine wave has been offset slightly to make it possible to see the two waves as separate. Each | + | The scale for the blue sine wave has been offset slightly to make it possible to see the two waves as separate. Each waveform is two complete cycles, each consisting of an initial ‘’positive half cycle’’ (above the horizontal centerline) and a ‘‘negative half cycle’’ below the centerline. It is easy to see the relationship of the period to the frequency as the period of one cycle is 1 millisecond (one one-thousandth of a second) for a 1000 cycle-per-second (or one kilo-Hertz) sine wave. |
Period = 1/frequency | Period = 1/frequency | ||
Revision as of 14:23, 28 August 2012
Overview
The term "waveform" is used to describe the shape or "form" of a wave signal. The term "wave" is commonly used to describe a cyclical electromagnetic signal or acoustic signal because of the similarity to "waves" in a body of water.
Basics
At the most basic level, a “sine” waveform represents a single frequency or “pure tone.” Most audio waveforms consist of multiple frequencies with varying phase relationships; which results in a very different shape than a sine wave. Using the technique of Fourier analysis; even complex waveforms can be broken-down into the constituent sine wave components.
For more information on Fourier analysis; click here.
Because the constituent sine waves of a complex waveform add or subtract from each other due their phase relationship; the shape of the waveform can vary over time; even if the amplitude and frequency of the constituent sine waves do not. In a similar manner, even if the waveform consists purely of harmonic frequencies; the phase relationship of each harmonic frequency component will affect the shape of the resulting complex waveform. This is part of the reason why using square waves with a near zero rise-time or extremely short impulses in testing audio circuitry is usually not relevant to circuit performance with audio signals. The only way a "square edge" waveform can exist is if every harmonic frequency remains perfectly "in-phase" with each other, and harmonics extending into the hypersonic frequencies are included. Although it is possible to generate square or square-edge pulse waveforms using a synthesizer or test equipment; real-world music (and most other audio) never contains square edge waveforms because limiting the signal's frequency response will result in a finite rise-time (or in other words a less than infinitely steep slope to the rising edge of the waveform). Virtually all audio is frequency-band limited for a number of reasons; including real limitations in audio performance caused when higher-than-audio frequencies are allowed to pass though audio amplifiers or digital audio converters.
for more information on hypersonic frequencies in digital audio, click here
Examples
The scale for the blue sine wave has been offset slightly to make it possible to see the two waves as separate. Each waveform is two complete cycles, each consisting of an initial ‘’positive half cycle’’ (above the horizontal centerline) and a ‘‘negative half cycle’’ below the centerline. It is easy to see the relationship of the period to the frequency as the period of one cycle is 1 millisecond (one one-thousandth of a second) for a 1000 cycle-per-second (or one kilo-Hertz) sine wave.
Period = 1/frequency
These two sine waves are “in-phase” and of the same polarity. Although Phase is a time domain difference between two audio waveforms; it is typically referred to in the number of degrees of difference. This is because each cycle of a periodic waveform contains 360 degrees; regardless of the frequency. For example; the period of a 2kHz sine wave is exactly one-half the time value of a 1kHz waveform; but they both are exactly at one-half a cycle 180 degrees from when they start.
A zero difference in time means the two waveforms are perfectly “in-phase.” If these two sine waves were summed (or “mixed”) at the same level; the result would be a sine wave at the same frequency with twice the amplitude, “in-phase” with the original waves.
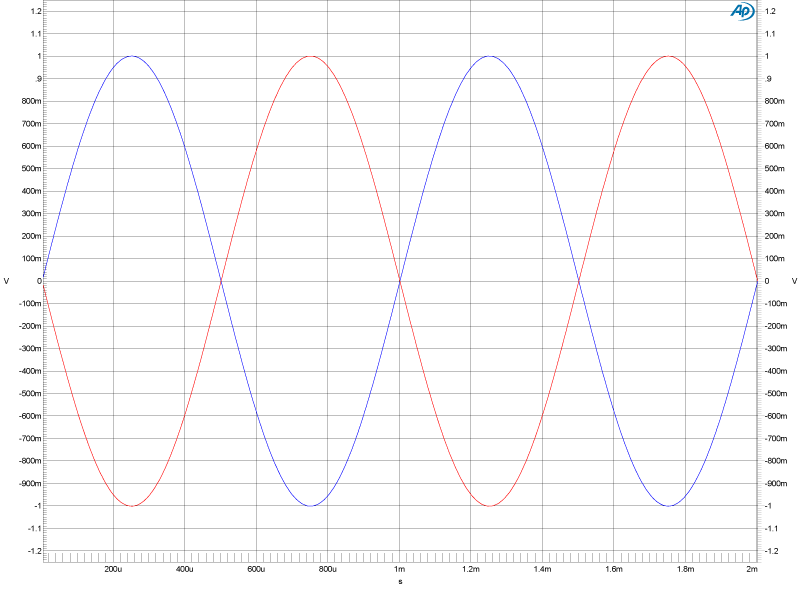
These two sine waves are either “out-of-phase” and of the same polarity or “in-phase” and of opposite polarity (the red sine wave can be seen as having inverted polarity). Because it is not possible to see the instant when these two sine waves began; it is not possible to determine their phase relationship. For example; they could either be in-phase and of opposite polarity, or 180 plus (N) times 360 degrees out-of-phase (540 degrees, 900 degrees, 1,260 degrees; etc.) This is a good illustration of how phase is relative (a difference in timing) and polarity is absolute (“normal” or “inverted”).
Because they are perfectly “out-of-phase” with each other (or of opposite polarity); if these two sine waves were summed, the result would be no signal because they would cancel each other completely. Even a small difference in amplitude would result in a sine wave of the same frequency with an amplitude equal to the difference (in amplitude) and phase matching the larger of the two sine waves. In other words, the “phase cancellation” would not be complete, and some of the larger signal would remain.
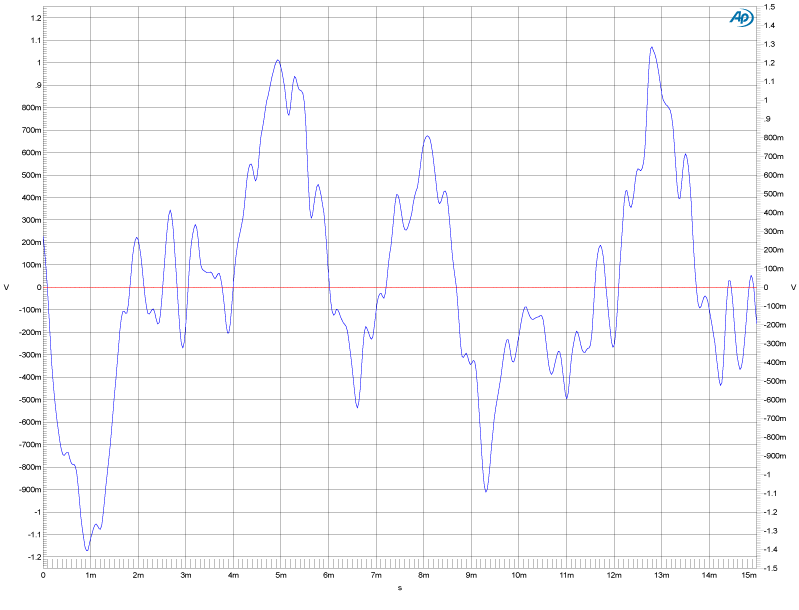
This is a “snapshot” of a brief section of a music waveform that contains many different frequencies in different phase relationships to each other. Please note that the time scale has been change from the sine wave graphs to show a range of frequencies. Careful observation shows what appear to be sections of sine waves superimposed on the peaks or valleys of large waves. This is a good illustration of how the phase relationship of the higher frequency waves determines whether they add or subtract from the shape of the larger (lower frequency) waves.